Real-Time Control for Nonlinear Systems
In this project, I developed computationally efficient optimal nonlinear control methods. I developed numerical techniques that can run in real-time for high dimensional nonlinear systems with provable guarantees of convergence, stability, and near optimality. I have also shown that the existence of these optimizers depends on local nonlinear controllability.
Convergence
I derived a nonlinear feedback control synthesis that has formal guarantees
on controllability-dependent convergence. Using optimal perturbations,
the algorithm avoids expensive iterative computations, is
faster than alternative state-of-the-art controllers, and can run in real time.
Fish, like cars, do not have the ability to move directly sideways;
such motion requires a combination of different motions. The algorithm
I designed automatically computes the required sequences of actions
to complete such moves. This is a parallel maneuver of an underactuated
dynamic 3D fish that cannot move sideways, downwards, or pitch. The algorithm,
in real-time, pushes the fish sideways by combining roll and upward motion, while alternative
solutions fail.
Being able to compute solutions matters especially
in time-critical operations. In the presence of a constant fluid drift,
failing to find solutions can be disastrous. In the demo on the right,
my algorithm can find solutions to move the fish against the flow and stay
close to the target.
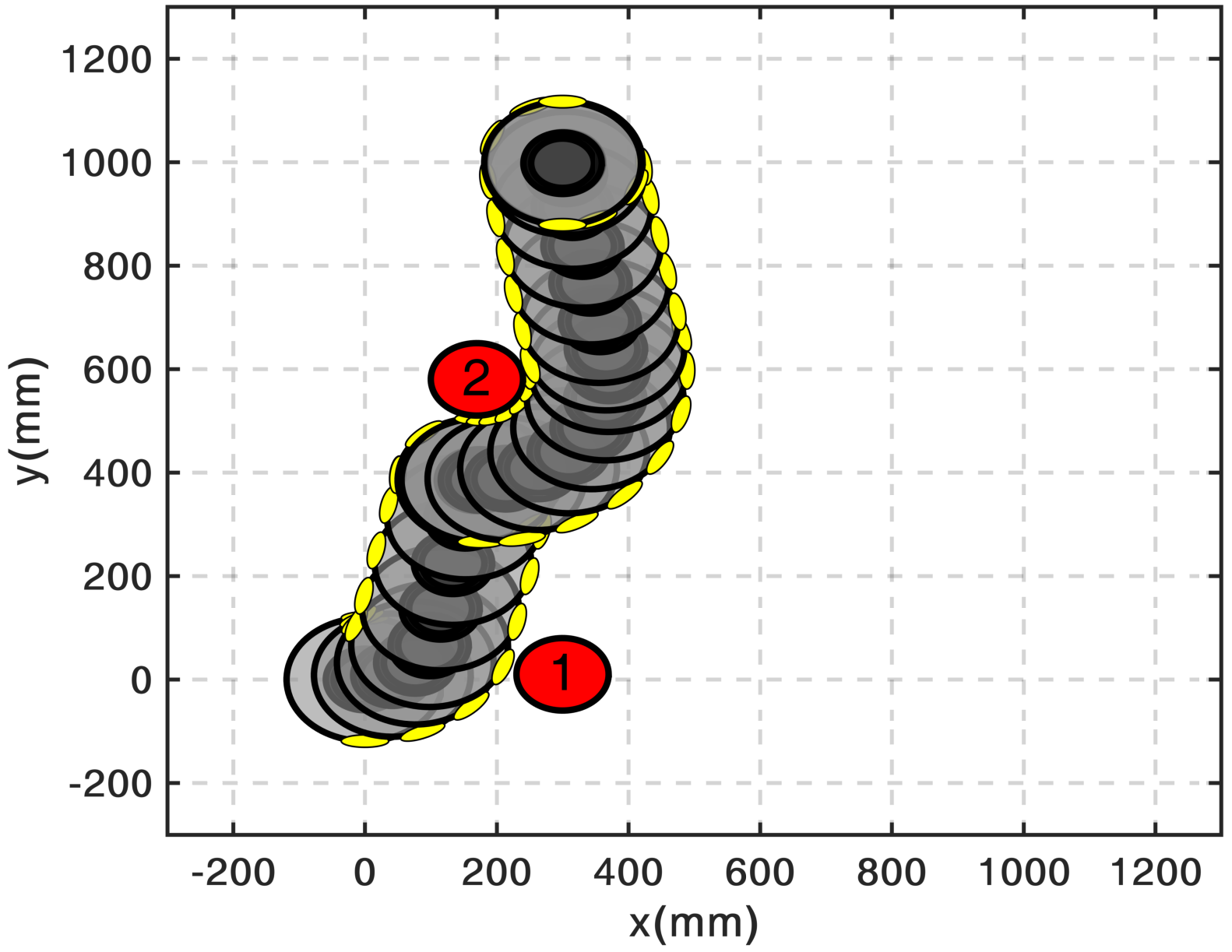
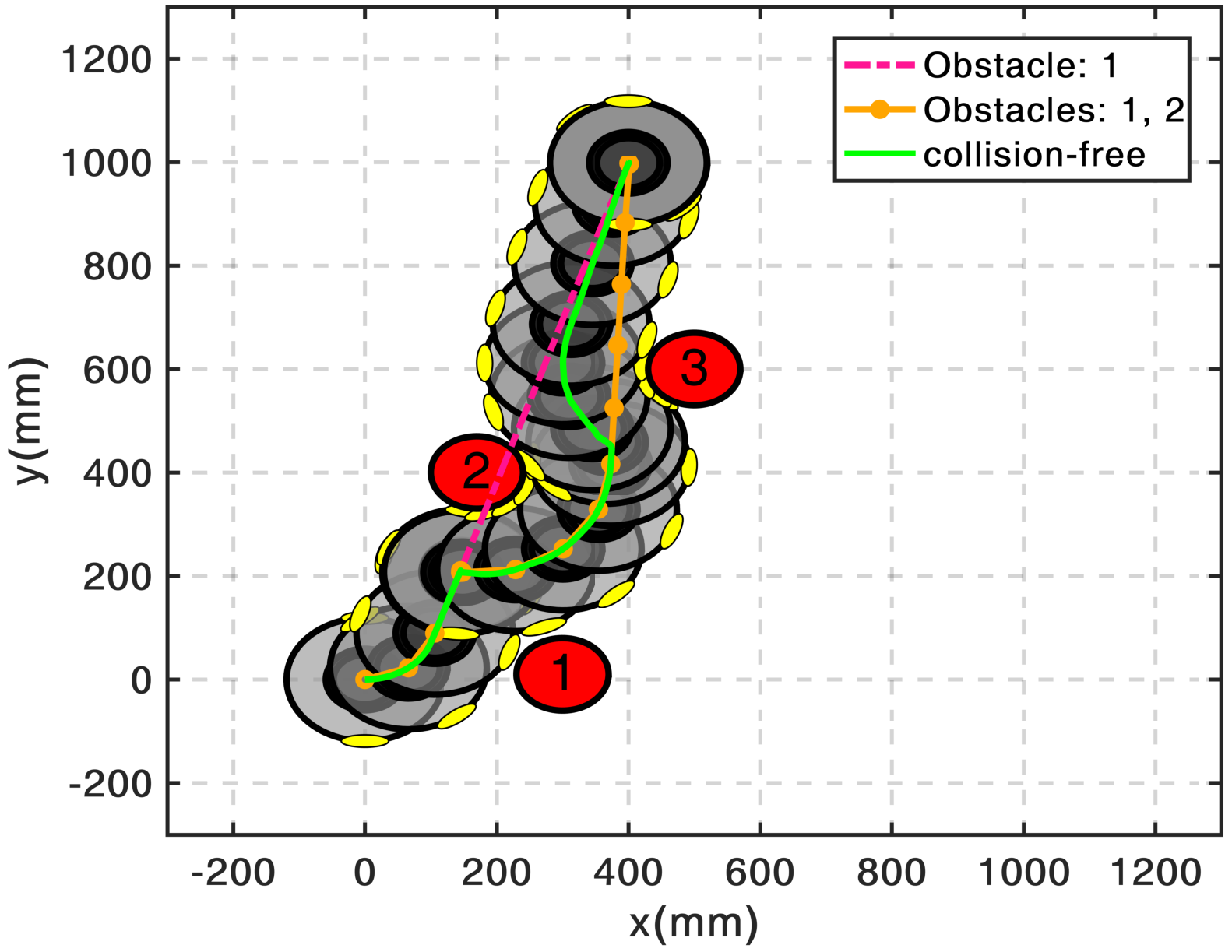
Path planning amidst obstacles is often treated separately from the optimal control problem; algorithms
find a collision-free path first and then try to move a system along that solution. The algorithm I designed
addresses both problems together and computes motions that have guarantees on being collision-free.
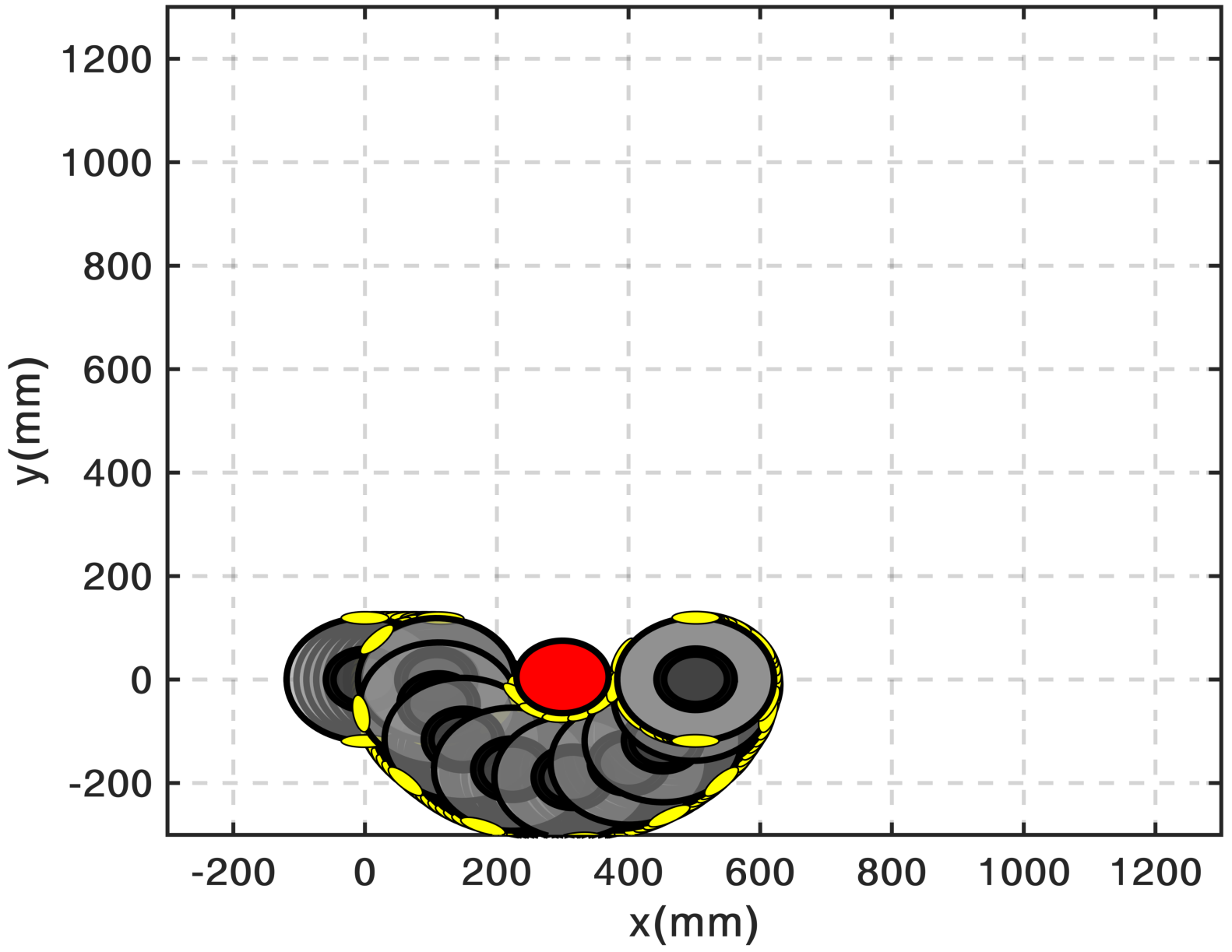
For illustration pursposes, I use the iRoomba robot as a differential drive model to demonstrate some
maneuvers among obstacles. In the video, I show the path followed by the model to reach the target starting
from several different positions. The algorithm, in real-time, always finds the best paths, even through narrow spaces (between obstacles 2 and 3).
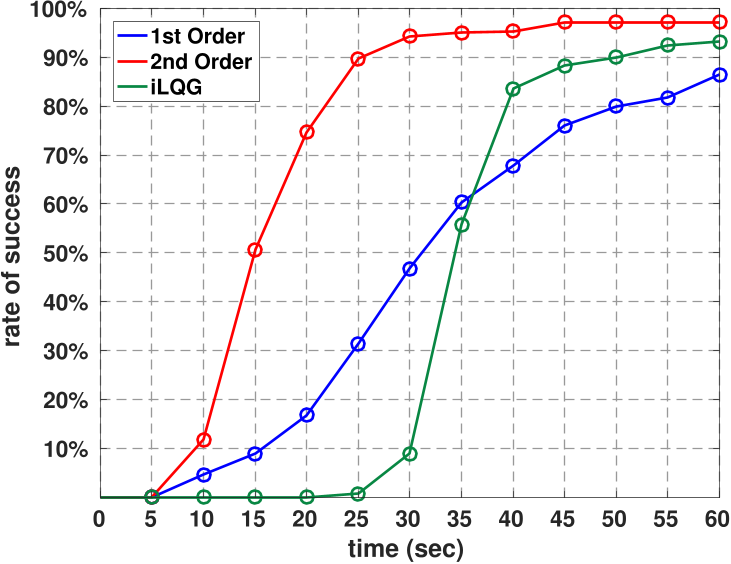
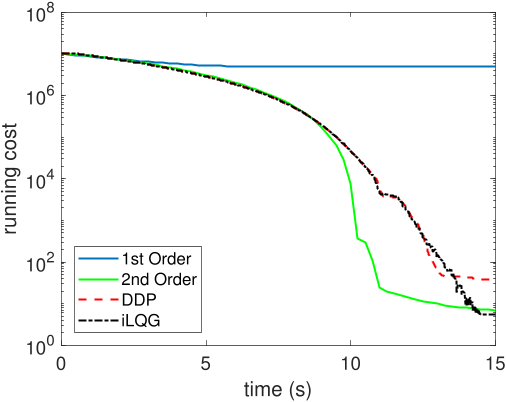
Besides guaranteeing solutions when other methods fail, the designed algorithm is shown to have qualitatively better solutions than alternative schemes and converge faster.
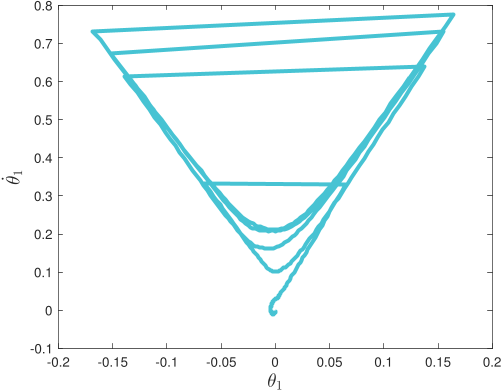
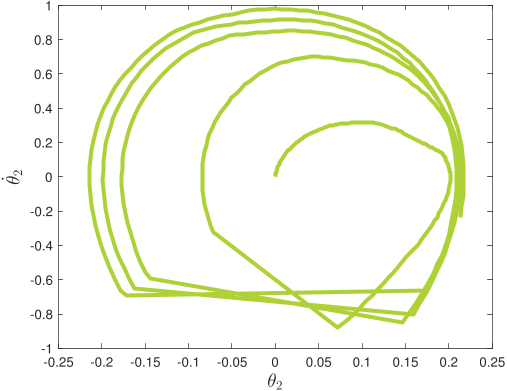
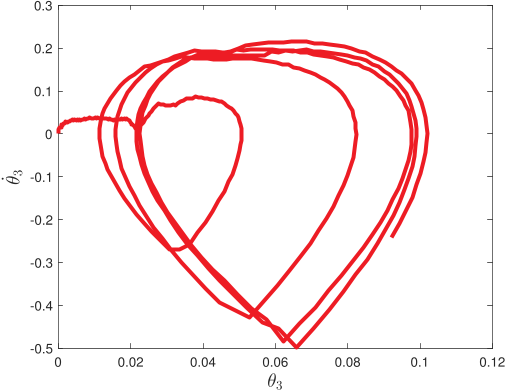
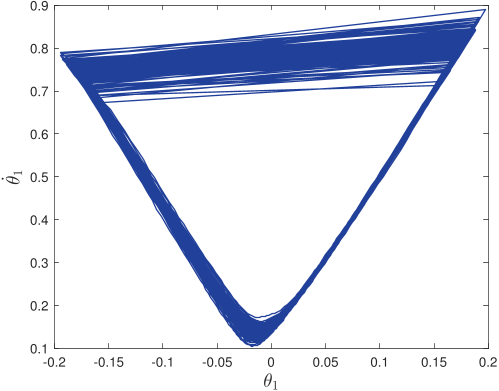
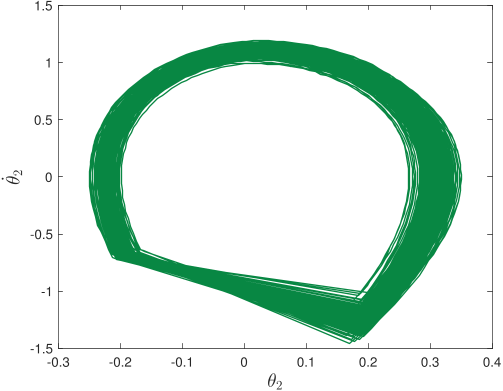
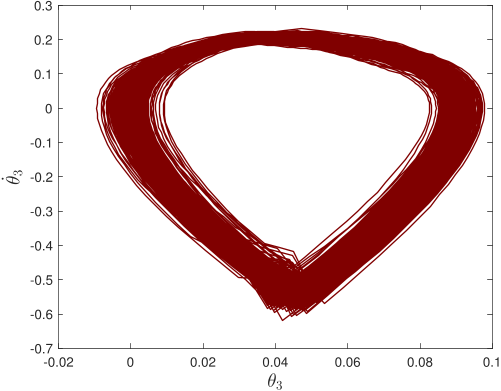
Without pre-specified gait initiliazation, the algorithm is able to establish a quasi-periodic gait. In the phase plots above, the top line corresponds to the first ten seconds of the gait initialization
and the bottom one to the remaining 5-minute walk simulation.
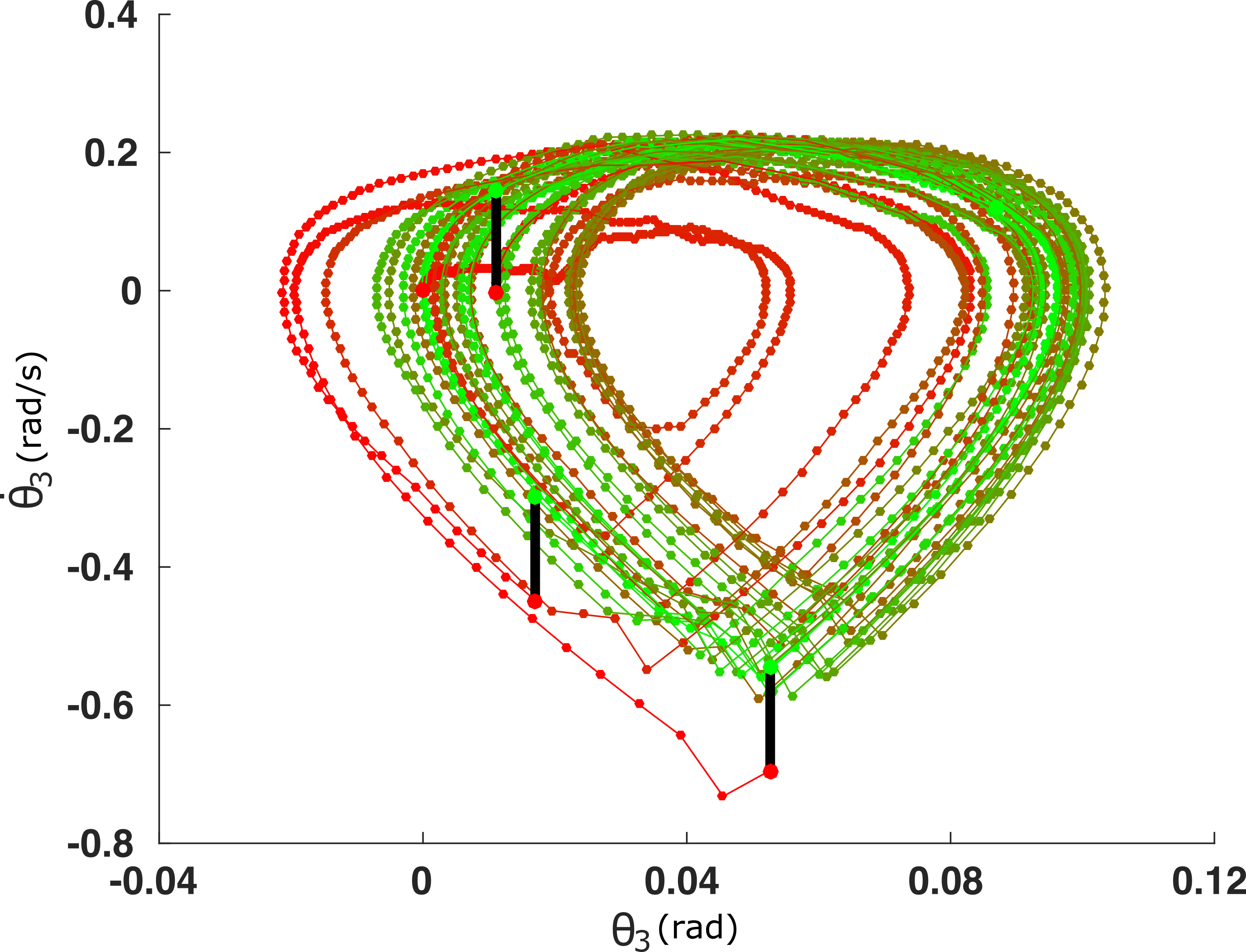
Further, the algorithm is robust against torso disturbances (introduced as discontinuities in its angular velocity).
After each push, the controller recovers its quasi-periodic gait.
Feedback synthesis for underactuated systems using sequential second-order needle variations
Superlinear convergence using controls based on second-order needle variations
Feedback synthesis for controllable underactuated systems using sequential second order actions
This project was funded by the Office of Naval Research and the National Science Foundation–Civil and Mechanical Systems: Stability and Optimality Properties of Sequential Action Control for Nonlinear and Hybrid Systems.
Obstacle Avoidance

Convergence Rate
In simulations of a three-link bipedal walking, the algorithm is shown to successfully
perform gait initiation, walking, and disturbance tolerance.

Selected Publications
G. Mamakoukas, M. Maciver, and T. D. Murphey
International Journal of Robotics Research (IJRR), vol. 37, no. 13-14, pp. 1826–1853, 2019. PDF
G. Mamakoukas, M. MacIver, and T. D. Murphey
IEEE International Conference on Decision and Control (CDC), pp. 4301–4308, 2018. PDF
G. Mamakoukas, M. MacIver, and T. D. Murphey
Robotics: Science and Systems Proceedings (RSS), 2017. PDF, VideoFunding